グラフのchain decompositionと、それを使って橋と関節点を求める手法のメモ
橋と関節点を求める手法といえばlowlinkを用いた手法が存在するが、他の手法としてchain decompositionを用いた手法が存在する。(WikipediaのBridge (graph theory)とBiconnected componentに載っている)
以下を参考にしている
[1] Schmidt, Jens M. "A simple test on 2-vertex-and 2-edge-connectivity." Information Processing Letters 113.7 (2013): 241-244.
chain decompositionとは
chain decomposition はDFS-treeをベースにグラフをpathもしくはcycle (= chain)に分けた上で、2-edge-connectivity(1つの辺を除去しても連結)もしくは2-connectivity(1つの頂点を除去しても連結)を判定する線形時間のアルゴリズム。
この chain decomposition では ear decomposition を計算しており、グラフが 2-edge-connected であれば ear decomposition となり、2-connected であれば open ear decomposition となる。
この判定を利用し、橋もしくは関節点を列挙することができる。
構築方法
グラフGのchain decompositionは以下のようにして求める。
1. グラフGを根付き木としてDFSし、DFS-treeを求める
- この時、treeに含まれる辺をtree edge、含まれない辺をbackedgeとする
- tree edgeを根頂点に向かう有向辺、backedgeを根頂点から離れる有向辺とする
2. DFSで訪ねた頂点をpre-orderの順序で見ていき、各頂点を始点とする各backedgeに対するchainを求める
chainは以下のように求める (現在見ている頂点をvとする)
- 頂点vが始点となる各backedgeについて、そのbackedgeの終点の頂点wからtree edgeを伝って頂点vへと遡っていく
- この時、各頂点にはvisitフラグをつけておく
- 到達した頂点に既にvisitフラグが立っているか、頂点vに到達した場合は探索を停止
- 頂点wから探索を停止した頂点xまでのpath(もしくは頂点vまで探索できた場合のcycle)を1つのchainとする
この時、番目に見たbackedgeから求めたchainを
とする
3. 各backedgeから求めたchainの集合をchain decomposition とする
- chainは
個(backedgeの数だけ)存在する
例として以下のグラフを考える。
このグラフ上で一番上の頂点からDFSを行い、tree edgeとbackedgeを得る。以下の図の黒い辺がtree edge、赤い辺がbackedgeである。頂点についている番号はpre-orderの順序。
そして、このDFSのpre-orderの順序で各backedgeに対するchainを得る。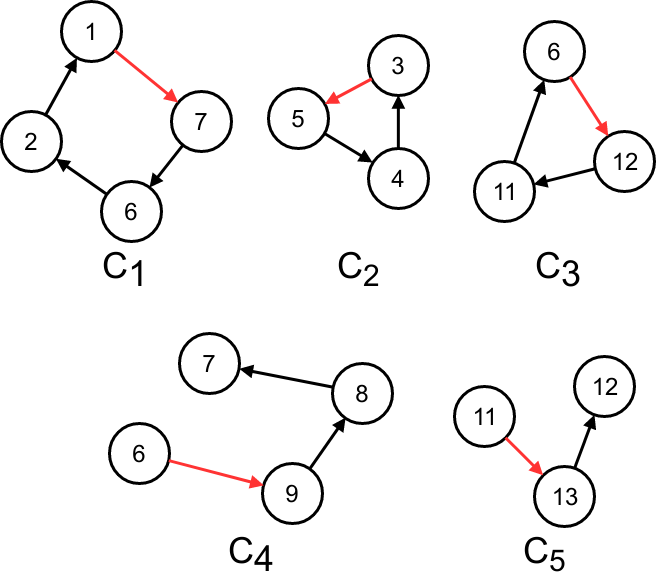
このchain decompositionは で得ることができる。
橋の列挙
このchain decompositionがグラフの辺の分割(partition)となる場合、2-edge-connectedであると判定できる。
2-edge-connectedでない場合は橋が存在し、この橋は任意のchain に含まれていない辺を列挙することで求められる。
例のグラフにおける橋はchain decompositionに含まれていない、以下の図で橙丸で囲った辺が該当する。
関節点の列挙
グラフの全頂点の次数が2以上であり、かつchain decompositionに含まれるcycleが
のみである場合、グラフは2-connectedであると判定できる。
2-connectedでない場合は関節点が存在し、関節点は以下のいずれかを満たす次数が2以上の頂点が該当する。(次数1の頂点は除去しても非連結にならない)
1. 橋となる辺に隣接する頂点
2. 以外でcycleとなるchain
の、探索を開始したbackedgeの始点となる頂点
例のグラフでは、橋に隣接する頂点2, 9と cycleのchain のbackedgeの始点である頂点3, 6が関節点になることが分かる。橋に隣接する頂点10は次数1であるため、関節点にはならない。

実装
連結グラフに対する橋と関節点を計算する。
# chain decomposition の構築 def construct(G, N): # P[v]: DFS-treeにおける頂点vの親頂点 P = [0]*N # G0: グラフGのbackedgeのみに絞った有向グラフ G0 = [[] for i in range(N)] # V: 頂点をpre-orderに並べたもの V = [] # P, V, G0 を計算するDFS lb = [0]*N def dfs(v, p): P[v] = p V.append(v) lb[v] = len(V) for w in G[v]: if w == p: continue if lb[w]: if lb[v] < lb[w]: # (v, w) は backedge G0[v].append(w) continue # (v, w) は tree edge dfs(w, v) dfs(0, -1) # B: 橋となる辺e = (u, v) のリスト B = [] # ap[v]: 頂点vが関節点であるか? ap = [0]*N used = [0]*N first = 1 used[0] = 1 # グラフの頂点をpre-orderで見ていく for u in V: if not used[u]: # 頂点uは以前に探索されてない # -> この親頂点pへのtree edgeがchainとして含まれない # -> 辺(u, p) は橋 p = P[u] B.append((u, p) if u < p else (p, u)) # 橋に隣接し、次数が2以上の頂点は関節点 if len(G[u]) > 1: ap[u] = 1 if len(G[p]) > 1: ap[p] = 1 # 頂点vが始点となるbackedgeについて調べる cycle = 0 for v in G0[u]: # tree edgeに従って根頂点に向かって上がっていく w = v while w != u and not used[w]: used[w] = 1 w = P[w] # このchainはcycle if w == u: cycle = 1 if cycle: if not first: # 2つ目以降のcycle chainである場合、頂点uは関節点 ap[u] = 1 first = 0 A = [v for v in range(N) if ap[v]] return B, A # B: グラフGの橋 # A: グラフGの関節点 B, A = construct(G, N)
Verified
- AOJ: "GRL_3_A: Connected Components - Articulation Points"
- AOJ: "GRL_3_B: Connected Components - Bridges"