CodeChef October Challenge 2019: Fun with Lists - 日々ｄｒｄｒする人のメモ

CodeChef October Challenge 2019の問題: Fun with Lists (Code: TANDON)
この問題は、他からのコピーだったという理由より問題が気づいたら消えてた。

They removed TANDON! - CodeChef Discuss
Forumによれば、以下の問題と同じらしい。
Reverse | Matrix Exponentiation & Math Practice Problems | HackerEarth

とりあえず解いたので書いておく。

問題概要

整数 $X$ をとり、その桁を逆順にした整数を返す $rev(X)$ を定義する。
( $rev(123) = 321$ , $rev(800) = 8$ )

$N$ 桁以下の $K$ の倍数の整数 $X$ のうち、 $rev(X)$ も $K$ の倍数になる整数の個数をmodulo $10^9 + 7$ で求めよ。

制約

1つのテストケースに含まれるケース数: $1 \le T \le 20$
$1 \le N \le 10^9$
$2 \le K \le 10$

解法

行列累乗で計算する。

まずDPで求めることを考えると以下で計算できる。

$dp[i][x][y] =$ $i$ 桁以下の整数 $X$ の中で余りが $x$ で $rev(X)$ の余りが $y$ となる整数の個数

このDPの計算量は $O(N K^3)$

次に行列を用いて計算する方法を考える。

まず、 $K^2$ 個の要素を持つベクトル $\mathbf{x}$ を考える。
整数 $X$ の中で余りが $x$ で $rev(X)$ の余りが $y$ となる整数の個数を $xK + y$ 番目の要素で表す。

初期値は 1,2, ..., 9 を含む状態にする。(0にすると10倍した時に0が重複するため計算がややこしくなるため、除いて最後に+1する)

具体的にベクトル $\mathbf{x}$ において

$x = y > 0$ となる要素を 1
それ以外の要素を 0

とする。

そして、状態を遷移させるための $K^2 \times K^2$ の行列を考え、 $d$ 桁目の計算では各 $0 \le a \le 9$ について $(x, y) \rightarrow (10x + a, 10^da + y)$ に遷移させるようにする。
(行列の $( (10x+a \bmod K)K + (10^da + y \bmod K) )$ 行 $(xK + y)$ 列を1にする)
この行列の $2 \le d \le N$ について $d = 2$ から順に $\mathbf{x}$ との積をとる必要があるが、各桁 $d$ における $(x, y)$ の遷移先は $10^d \bmod K$ の値で区別されるため、 $\mathbf{x}$ との積をとる行列の種類は高々 $K$ 種類になる。
$10^d \bmod K = v$ となる場合の行列を $D_v$ とする。

以下は各 $\bmod K$ における $10^d$ の値である。

K\d	0	1	2	3	4	5	6	7
2	1	0	0	...
3	1	1	...
4	1	2	0	0	...
5	1	0	0	...
6	1	4	4	...
7	1	3	2	6	4	5	1	...
8	1	2	4	0	0	...
9	1	1	...
10	1	0	0	...

$K \not = 7$ の場合は $10^d \bmod K$ の値は小さい $d$ を除き一定になり、 $K = 7$ の場合は周期6で循環する。

$K \not = 7$ の場合

$D_0, D_1, D_4$ の行列累乗( $D_v^N \mathbf{x}$ )を計算することで $N$ 桁目について $O(K^6 \log N)$ で計算できる。
ただし、今回必要なのは $N$ 桁目以下であり、
$S_N = D_v^N + D_v^{N-1} + ... + D_v + I$
とするとき、 $S_N \mathbf{x}$ を計算する必要がある。

これは、行列を要素に持つ2×2の行列累乗によって計算できる。(このテクニックは(形は違うが)蟻本に載ってるやつ)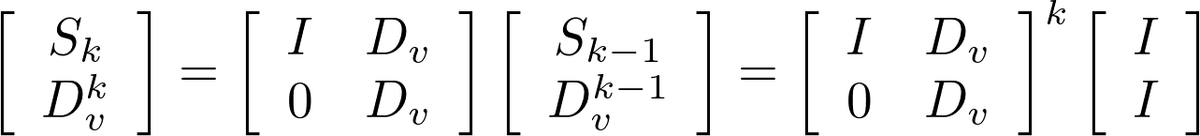

f:id:smijake3:20191020184606p:plain:w320 — $S_k$ を計算する行列累乗

$K = 7$ の場合

$10^d (\bmod 7)$ は 1, 3, 2, 6, 4, 5, 1, 3, 2, ... と長さ6で循環することを利用し、以下で求められる。

以下を前計算
- $R = D_1D_5D_4D_6D_2D_3$
- $T = D_1D_5D_4D_6D_2D_3 + D_5D_4D_6D_2D_3 + D_4D_6D_2D_3 + D_6D_2D_3 + D_2D_3 + D_3$
$L = \lfloor \frac{N-1}{6} \rfloor$ とするとき、 $R_S = R^{L-1} + R^{L-2} + ... + R^0$ を計算し、 $TR_S\mathbf{x}$ を計算 (これで $6L + 1$ 桁以下まで計算できる)
残りの $6L + 2$ 桁目から $N$ 桁目までは1つずつ計算していく

0 と 7 は解に含まれていないので、+2する。

全体の計算量は $O(K^6 \log N)$

実装

上の行列累乗を単純に実装したらTLEしたので少し計算を端折って高速化してる。

#define K 10

const ll mod = 1000000007;
int n, k, b, f;

ll res[K*K][K*K], temp[K*K][K*K];
ll base[K][K*K][K*K], base_d[K][K*K][K*K], base_x[K*K][K*K], base_s[K*K][K*K];

// 行列の積を計算 (A B = C)
inline void mul(ll mat_a[K*K][K*K], ll mat_b[K*K][K*K], ll mat_c[K*K][K*K]) {
  rep(p, k*k) rep(q, k*k) {
    mat_c[p][q] = 0;
    rep(r, k*k) {
      mat_c[p][q] += mat_a[p][r] * mat_b[r][q] % mod;
    }
    mat_c[p][q] %= mod;
  }
}

// 行列の和を計算 (A + B = C)
inline void add(ll mat_a[K*K][K*K], ll mat_b[K*K][K*K], ll mat_c[K*K][K*K]) {
  rep(p, k*k) rep(q, k*k) {
    mat_c[p][q] = (mat_a[p][q] + mat_b[p][q]) % mod;
  }
}

// 10^d ≡ bs (mod K) となる場合の行列を生成
inline void mat_gen(ll mat[K*K][K*K], ll bs) {
  rep(p, k*k) rep(q, k*k) mat[p][q] = 0;
  rep(x, k) rep(y, k) {
    rep(a, 10) {
      mat[((10*x+a) % k) + k*((bs*a+y) % k)][x+k*y] += 1;
    }
  }
}

ll temp0[K*K][K*K], temp1[K*K][K*K];
// 行列を要素に含む行列同士の積を計算
inline void mulmul(ll mat_a[4][K*K][K*K], ll mat_b[4][K*K][K*K], ll mat_c[4][K*K][K*K]) {
  auto xa = mat_a[0], xb = mat_a[1], xc = mat_a[2], xd = mat_a[3];
  auto ya = mat_b[0], yb = mat_b[1], yc = mat_b[2], yd = mat_b[3];
  auto za = mat_c[0], zb = mat_c[1], zc = mat_c[2], zd = mat_c[3];

  // 1行1列は常に I であるため計算しない
  //mul(xa, ya, temp0);
  //mul(xb, yc, temp1);
  //add(temp0, temp1, za);

  // xa は常に I なので計算を端折る
  //mul(xa, yb, temp0);
  mul(xb, yd, temp1);
  //add(temp0, temp1, zb);
  add(yb, temp1, zb);

  // 2行1列は常に 0 であるため計算しない
  //mul(xc, ya, temp0);
  //mul(xd, yc, temp1);
  //add(temp0, temp1, zc);

  // xc は常に 0 であるため計算を端折る
  //mul(xc, yb, temp0);
  //mul(xd, yd, temp1);
  //add(temp0, temp1, zd);
  mul(xd, yd, zd);
}

ll mat_xx[4][K*K][K*K], mat_temp[4][K*K][K*K];
ll mat_res[4][K*K][K*K];
// I + R + R^2 + ... + R^m を求める
inline void calc(ll mat_r[K*K][K*K], int m, ll mat_rr[4][K*K][K*K]) {
  // M_XX = [E1, R, E0, R]
  rep(p, k*k) rep(q, k*k) mat_xx[0][p][q] = 0;
  rep(i, k*k) mat_xx[0][i][i] = 1;
  rep(p, k*k) rep(q, k*k) mat_xx[1][p][q] = mat_xx[3][p][q] = mat_r[p][q];
  // M_RR = [E1, E0, E0, E1]
  rep(p, k*k) rep(q, k*k) mat_rr[0][p][q] = mat_rr[1][p][q] = mat_rr[3][p][q] = 0;
  rep(i, k*k) mat_rr[0][i][i] = mat_rr[3][i][i] = 1;
  // calc (M_XX)^m
  while(m > 0) {
    if(m & 1) {
      mulmul(mat_rr, mat_xx, mat_temp);
      rep(i, k*k) rep(j, k*k) mat_rr[1][i][j] = mat_temp[1][i][j];
      rep(i, k*k) rep(j, k*k) mat_rr[3][i][j] = mat_temp[3][i][j];
    }
    mulmul(mat_xx, mat_xx, mat_temp);
    rep(i, k*k) rep(j, k*k) mat_xx[1][i][j] = mat_temp[1][i][j];
    rep(i, k*k) rep(j, k*k) mat_xx[3][i][j] = mat_temp[3][i][j];
    m >>= 1;
  }
}

int main() {
  int t; cin >> t;
  ll res;

  while(t--) {
    cin >> n >> k;

    if(k != 7) {
      if(k == 3 || k == 9) {
        mat_gen(base_x, 1);
      } else if(k == 6) {
        mat_gen(base_x, 4);
      } else {
        // k = 4, 8 における d = 1, 2 の場合も D_0 で計算すると解が一致するため、D_0 でまとめて計算
        mat_gen(base_x, 0);
      }
      res = 1;
      calc(base_x, n-1, mat_res);
      repl(e, 1, 9) {
        int v = e % k;
        res += (mat_res[0][0][v+k*v] + mat_res[1][0][v+k*v]);
        res %= mod;
      }
    } else {
      int bs = 10 % k;
      // 前計算
      // 各行列 D_v を用意
      rep(i, k-1) {
        // base[i] = 10^{i+1} (mod 7)
        mat_gen(base[i], bs);
        bs = 10 * bs % k;
      }
      // base_d[i] = base[0] * base[1] * ... * base[i]
      rep(i, k*k) rep(j, k*k) {
        base_d[0][i][j] = base[0][i][j];
      }
      repl(i, 1, k-2) {
        mul(base[i], base_d[i-1], base_d[i]);
      }
      // base_s[i] = base_d[0] + base_d[1] + ... + base_d[i]
      rep(i, k*k) rep(j, k*k) {
        base_s[i][j] = base_d[0][i][j];
      }
      repl(l, 1, k-2) {
        rep(i, k*k) rep(j, k*k) {
          base_s[i][j] = (base_s[i][j] + base_d[l][i][j]) % mod;
        }
      }

      res = 2;

      int k0 = (n-1) / (k-1);
      calc(base_d[k-2], k0-1, mat_res);
      if(k0 > 0) {
        // base_x は R_s になる
        add(mat_res[0], mat_res[1], base_x);
        // T R_s を計算して temp0 にする
        mul(base_s, base_x, temp0);
        // T R_s x を求める
        repl(e, 1, 9) {
          int v = e % k;
          res += temp0[0][v+k*v];
          res %= mod;
        }
        //add(mat_res[2], mat_res[3], temp0);
        //mul(base_d[k-2], temp0, base_x);
        mul(base_d[k-2], mat_res[3], base_x);
      } else {
        rep(i, k*k) rep(j, k*k) base_x[i][j] = 0;
        rep(i, k*k) base_x[i][i] = 1;
      }

      // 残りは1回ずつ計算していく
      repl(i, k0*(k-1), n-2) {
        mul(base[i % (k-1)], base_x, temp0);
        rep(p, k*k) rep(q, k*k) {
          base_x[p][q] = temp0[p][q];
        }
        repl(e, 1, 9) {
          int v = e % k;
          res += base_x[0][v+k*v];
          res %= mod;
        }
      }
    }
    cout << res << "\n";
  }
  return 0;
}