LCAをベースに構築するAuxiliary Treeのメモ - 日々ｄｒｄｒする人のメモ

(2019/09/15 20:50頃追記) ただAuxiliary Treeと書くと(一般的すぎて)齟齬を生む可能性が高いので、タイトル及び一部文章を変更しました。申し訳ないです。今回はLCAをベースに構築するAuxiliary Treeについて取り上げてます。

最近、LCAを元に構築する Auxiliary Tree を使う問題に出会ったので書いた。

CodeChef July Challenge 2019 で以下の問題があった。

smijake3.hatenablog.com

自分は Auxiliary Tree を使わず解いたが、想定解法が Binarization of a tree + Centroid Decomposition on Edge + Auxiliary Tree だったらしい。

discuss.codechef.com

以下を参考にしている。

LCAをベースに構築するAuxiliary Treeとは
構築方法
実装
関連する問題

LCAをベースに構築するAuxiliary Treeとは

この木は Virtual Tree (虚树) とも呼ばれるらしい。

LCAをベースに構築する Auxiliary Tree は特定の頂点集合 $X$ とそれらのLCAのみを含みながら、頂点同士の関係を失わないように木を圧縮したものである。

f:id:smijake3:20190909232711p:plain — LCAをベースに構築するAuxiliary Treeのイメージ
(左が元の木、右がそのAuxiliary Tree)

このAuxiliary Treeの頂点数は頂点集合 $X$ のサイズに比べて高々2倍になり、構築は頂点集合 $X$ のサイズの準線形オーダーの計算量で可能である。
そのため、木 $T$ に対する多くのクエリが与えられるが、見るべき頂点の数がクエリ全体で限られている場合にこのテクニックを適用することができる。

例えば、以下のような問題が解ける。

Codeforces: 613D - Kingdom and its Cities
$N$ 頂点からなる木が与えられ、 $Q$ 個のクエリが与えられる。
$i$ 番目のクエリでは $k_i$ 個の頂点が与えられるので、この $k_i$ 個の頂点同士を非連結にするために( $k_i$ 個以外の頂点で)削除するべき頂点の最小個数を答えよ。
(不可能な場合は"-1")

制約

$1 \le N \le 10^5$

$1 \le Q \le 10^5$

$K = \sum_i k_i \le 10^5$

この問題は各クエリごとにDPをすると解くことができるが、各クエリごとに木全体を探索しながら計算すると $O(NQ)$ となり間に合わない。
それに対しLCAベースのAuxiliary Treeを使うことで、各クエリを $O(k_i \log k_i)$ で計算でき、全体で前計算含め $O(N \log N + K \log K)$ で計算できるため間に合うようになる。

構築方法

与えられた頂点集合 $X$ に対し、LCAベースのAuxiliary Treeは大雑把に以下の流れで構築できる。

頂点集合 $X$ をpre-orderの順序でソートしたリストを得る
ソートしたリストに対し、隣接する頂点のLCAを求める
頂点集合 $X$ と求めたLCAを元にstackを用いて木を構築する

具体的な方法を調べてたら以下の構築方法があったので、これらの方法を書いておく。

ソート1回、depthの関係からstackからpopする方法
ソート2回、Euler Tour上の頂点の位置関係からstackからpopする方法

ソート1回の方法

1回ソートしたリスト $x_1, x_2, ..., x_k$ について、 $i=0$ から $x_i$ と $x_{i+1}$ のLCAを求めながら、Auxiliary Treeを構築していく方法。

具体的な流れは以下のようになる。

はじめに空のstackに $x_0$ をpushし、 $x_1$ から処理を行う。
まで処理した後にを処理する場合、以下のようにstackを更新する。 (この時点のstackのtopはになる)
- $x_i$ と $x_{i+1}$ の LCA $w$ を求める
- stackのtopの頂点 $v$ について $depth_w \le depth_v$ を満たす間 pop を繰り返す
- 頂点 $w$ と頂点 $x_{i+1}$ を stack に push

各頂点の親頂点 $v$ は、stackにpushされた後、popされた時点での親頂点(stackの次のtop もしくは頂点 $w$ )になる。
また、popされずに頂点 $x_k$ まで処理を完了した時点でstackに残っている頂点 $v$ の親頂点は、その時点のstackの並びから分かる。

ここで具体例を考える。
以下のような木を考え、頂点2, 6, 9, 12を含むAuxiliary Treeを構築するとする。

ここでは、頂点2, 6, 9まで計算し終わったとする。この時、stackはtopの方から頂点9, 頂点5, 頂点1が含まれる。

その次の頂点である頂点12を処理する。まず頂点9と頂点12のLCAを計算する(このLCAは頂点3である)。
次に、頂点3より深い頂点を全てpopする。ここでは、頂点9と頂点5がpopされる。(この時点で頂点9の親頂点が頂点5、頂点5の親頂点が頂点3であることが分かる)

頂点3と頂点12を順番にstackにpushし、頂点12までの処理を完了する。(この時点で頂点2, 6, 9, 12の全ての頂点を処理したので、stack上の頂点3と頂点12の親頂点も確定する)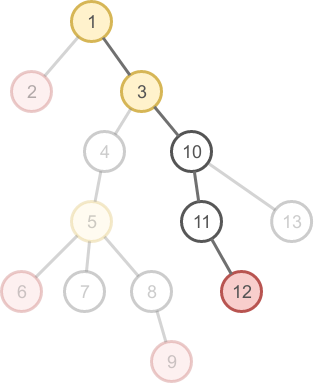

ソート2回の方法

この方法では、1回ソートした後に $x_i$ と $x_{i+1}$ の各LCAを一旦求める。その後、頂点集合 $X$ と求めたLCAを含めてもう一度ソートし、このソートされたリストを元にAuxiliary Treeを構築していく。
ここでは、2回ソートした後のリストを $y_1, y_2, ..., y_m$ (重複は除く、 $k \le m \le 2k-1$ )とする。

例えば、さっきの例と同じように頂点2, 6, 9, 12を含むAuxiliary Treeを構築する場合、2回ソートを行ったリスト(頂点1, 2, 3, 5, 6, 9, 12)を元に構築していく

次に、stackから頂点をpopする際の判定方法であるが、 $y_i$ と $y_{i+1}$ のLCAを求めてdepthをチェックしてもよいが、木 $T$ 上のEuler Tourにおける頂点の出現位置の関係を見ることでも判定できる。
具体的には、ETにおける頂点 $v$ の最初の出現位置を $first(v)$ 、最後の出現位置を $last(v)$ とする時、stackのtopの頂点 $v$ と現在処理している頂点 $y_i$ が $last(v) < first(y_i)$ を満たす(= 根頂点から頂点 $y_i$ のパス間に(今まで見ていた)頂点 $v$ が存在しない)限りpopすればよい。

下の図は、頂点9まで処理した後に頂点12を処理しようとする例であり、stackには頂点9, 5, 3, 1がtopから順に並んでいる。
下に示すET上では、 $last(9) < last(5) < first(12)$ を満たすことから、頂点9,5は根頂点と頂点12の間のパス上にないことが分かるため、stackからpopする。(頂点1, 3は $first(12) < last(3) < last(1)$ を満たすのでstackに残しておく)

f:id:smijake3:20190914181632p:plain — 頂点12を処理中の木(上)と木 $T$ のEuler Tourの列(下)

流れをまとめると、以下のように処理していく。

はじめに空のstackに $y_0$ をpushし、 $y_1$ から処理を行う。
まで処理した後にを処理する場合、以下のようにstackを更新する。 (この時点のstackのtopはになる)
- stackのtopの頂点 $v$ について $last(v) < first(y_{i+1})$ を満たす間 pop を繰り返す
- 頂点 $y_{i+1}$ を stack に push

各頂点 $v$ の親頂点は、stackにpushされる直前のstackのtopの頂点になる。

親頂点が決定しやすいという点でいえば、2回ソートの方が構築しやすい気がする。

計算量

頂点 $k$ 個の頂点集合 $X$ を含む、Auxiliary Treeの頂点は高々 $2k-1$ になる。
これより、前計算・構築する際の計算量は

各頂点のpre-orderを求める前計算に $O(N)$
pre-orderの順序のソートに $O(k \log k)$
リスト走査による構築に $O(k)$ × (LCA の計算量)

となる。

よって、クエリ全体で関係する頂点の数の合計を $K$ とした時、
LCAを求めるのに Euler Tour Technique + Sparse Table を用いることで、全体のAuxiliary Treeの構築は $O(N \log N + K \log K)$ でできる。

実装

1回ソート、2回ソートの両実装を書いた。

ETT + Sparse Table を用いた実装
実装は Python (C++実装は2回ソートの方を実装メモの方に載せてある)
各クエリを処理した後にAuxiliary Treeの隣接リストを初期化する必要がないように実装してある

前計算

Euler Tour Technique における計算: $O(N)$
Sparse Table の前計算: $O(N \log N)$

# FS[v]: ET上の頂点vの最初の出現位置
# LS[v]: ET上の頂点vの最後の出現位置
# depth[v]: 頂点vの深さ
FS = LS = depth = None
# lg[x]: log_2 x の値
lg = None
# st[lv][v]: Sparse Table
st = None

# 前計算 O(N log N)
# - LCAの前計算を行う
def construct(N, G):
    global FS, LS, depth, G0, lg, st

    # S: グラフG の Euler Tour
    S = []

    FS = [0]*N; LS = [0]*N
    depth = [0]*N
    # Euler Tour Technique
    def dfs(v, p, d):
        depth[v] = d
        FS[v] = len(S)
        S.append(v)
        for w in G[v]:
            if w == p:
                continue
            dfs(w, v, d+1)
            S.append(v)
        LS[v] = len(S)
        S.append(v)
    dfs(0, -1, 0)

    # Sparse Table の構築
    L = len(S)
    lg = [0]*(L+1)
    for i in range(2, L+1):
        lg[i] = lg[i >> 1] + 1

    st = [[L]*(L - (1 << i) + 1) for i in range(lg[L]+1)]
    st[0][:] = S
    b = 1
    for i in range(lg[L]):
        st0 = st[i]
        st1 = st[i+1]
        for j in range(L - (b<<1) + 1):
            st1[j] = (st0[j] if depth[st0[j]] <= depth[st0[j+b]] else st0[j+b])
        b <<= 1

Auxiliary Treeの構築 (ソート1回)

計算量は $O(k \log k)$

# LCAを求める O(1)
def lca(u, v):
    # 常に x < y を満たすため、 x > y の時のswap処理は入れてない
    x = FS[u]; y = FS[v]
    l = lg[y - x + 1]
    return st[l][x] if depth[st[l][x]] <= depth[st[l][y - (1 << l) + 1]] else st[l][y - (1 << l) + 1]

# Auxiliary Treeの構築 O(k log k)
# リストvsで与えられたk個の頂点からAuxiliary Treeを構築
#
# - 構築結果は G0 に入る
# - 計算後のリストvsにはAuxiliary Treeの頂点が全て含まれる
# - 返り値はAuxiliary Tree上の根頂点
def auxiliary_tree(k, vs, G0):
    vs.sort(key=FS.__getitem__)
    stk = [vs[0]]
    G0[vs[0]] = []

    # LCAを求めながら Auxiliary Tree を構築
    for i in range(k-1):
        w = lca(vs[i], vs[i+1])

        # vs[i] が vs[i+1] の祖先でない場合はstackからのpopを行う
        if w != vs[i]:

            # 頂点wより深い頂点を全て pop する
            # last: stackの最もtopの頂点を表す
            last = stk.pop()
            while stk and depth[w] < depth[stk[-1]]:
                # lastの頂点の親頂点が決まる
                G0[stk[-1]].append(last)
                # popすることでlastも更新
                last = stk.pop()

            # 頂点w の直下の頂点(last)を子頂点として決定
            if not stk or stk[-1] != w:
                stk.append(w)
                vs.append(w)
                G0[w] = [last]
            else:
                G0[w].append(last)

        stk.append(vs[i+1])
        G0[vs[i+1]] = []

    # stack上に残った頂点も親子関係を決定する
    for i in range(len(stk)-1):
        G0[stk[i]].append(stk[i+1])

    return stk[0]

Auxiliary Treeの構築 (ソート2回)

計算量は $O(k \log k)$

# LCAを求める O(1)
def lca(u, v):
    x = FS[u]; y = FS[v]
    l = lg[y - x + 1]
    return st[l][x] if depth[st[l][x]] <= depth[st[l][y - (1 << l) + 1]] else st[l][y - (1 << l) + 1]

# Auxiliary Treeを構築 O(K log K)
# リストvsで与えられたk個の頂点からAuxiliary Treeを構築
#
# - 構築結果は G0 に入る
# - 計算後のリストvsにはAuxiliary Treeの頂点が全て含まれる (重複あり, ソート済み)
# - 返り値はAuxiliary Tree上の根頂点
def auxiliary_tree(k, vs, G0):
    # 頂点をpre-orderの順序でソート
    vs.sort(key=FS.__getitem__)

    for i in range(k-1):
        # vs[i], vs[i+1] の LCA w を vs に追加
        vs.append(lca(vs[i], vs[i+1]))

    # LCAを追加した後にもう一度pre-orderの順序でソート
    vs.sort(key=FS.__getitem__)

    # Auxiliary Tree を構築
    stk = []
    prv = -1
    for v in vs:
        if v == prv:
            # 重複は処理しない
            continue
        # ET上で last(stk[-1]) < first(v) を満たす間stackから pop していく
        while stk and LS[stk[-1]] < FS[v]:
            stk.pop()
        # 頂点vの親頂点は、頂点vをstackにpushする時点で決定される
        if stk:
            G0[stk[-1]].append(v)
        G0[v] = []
        stk.append(v)
        prv = v
    return stk[0]