前回の記事の続き
smijake3.hatenablog.com
コドフォのSegment Tree Beatsの説明の例題として挙がっているTask 3,4を実装したので、そのあたりの考え方含めて書いておく
今回は考え方の説明がメインの記事。とりあえず自分が理解した(と思う)範囲で書いた。
例題については、方針の説明 + 実装コードになっている。
また、今回は主に以下を参考にして書いてある
- 区间最值操作与历史最值问题 - 道客巴巴 (3.2あたり)
※2019/05/28 計算量が間違ってる箇所があったため修正
目次
セグ木の各ノードで区間情報を分けて管理する
Segment Tree Beatsでは各ノードにおいて、区間が持つ情報を要素によって分けて管理しながらクエリを処理することができ、今回の例題も区間情報を分けて管理しながら処理をする。
ここでは、この考え方について説明する。
区間chminクエリを扱う問題
今回は、区間chminクエリとその他従来のクエリを扱う場合について考える。
また、以下の例題を元に説明していく。(この問題を解くためには区間が持つ情報を分割する必要がないが、説明のために分割することを考える)
長さ
の数列
が与えられる。以下のクエリを合計
回処理せよ。
について
の値を
に更新
について
の値を
に更新
を出力
制約:
区間の最大値・非最大値による区間情報の分割
Segment Tree Beatsで区間chminクエリを処理する際、((厳密な)二番目の最大値) < x < (最大値) を満たす各ノードについて、その最大値の要素に新しい最大値との差分を加算した上で区間が持つ情報(区間総和や区間最大値、等)を更新する。
この更新を行うノードでは 最大値の要素のみを(最大を維持するように)更新した上で、この最大値の要素に関する情報のみを更新することになる。逆に最大値以外の非最大値の要素や最大値に関係しない情報は更新しない。
この性質から、各ノードの区間に含まれる各要素 を最大値と非最大値の2種類に分け、区間が持つ情報(区間最大値や区間総和、遅延させている値(lazy tag)等)を最大値・非最大値ごとに分けて管理しながらクエリを処理できる。例えば、上の例題であれば総和を最大値の総和・非最大値の総和に分けて管理することができる。(この例では最大値の総和を
、非最大値の総和を
とする)
イメージとしては下図のようになる。青枠には最大値の要素、緑枠には非最大値の要素が含まれ、この枠の単位で区間が持つ情報(総和や最大値、遅延させている値、等)を管理する。

(青枠が最大値、緑枠が非最大値。ノード上に枠が存在しない場合は要素が存在しない)
このように最大値と非最大値に分けて管理することにより、区間chminクエリは ((厳密な)二番目の最大値) < < (最大値) を満たすノードに対する、最大値のみに絞った区間加算操作として処理できる。
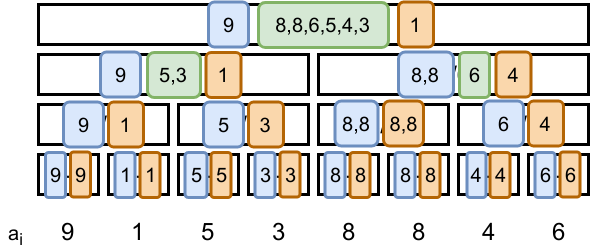
上の例題の区間chminクエリの更新について具体例で考えてみる。下の図は がとして8,8,4,6を含む区間を表し、この区間を
で更新した例である。この場合、最大値(青枠)の各要素に区間加算クエリとして-1 (= 7 - 8)を加算し、この加算値を元に(最大値のみの)区間総和
を更新することができる。

を適用した例
各クエリで処理すること
このように分割すると各クエリに対して以下のように処理できる。
- 区間chminクエリ:
- 区間加算クエリ(RAQ)や区間更新クエリ(RUQ)等の従来の操作クエリ
- 区間内の全てのノードを更新
- 各ノードの全ての要素を(遅延させながら)更新し、最大値と非最大値それぞれの情報を更新
- 区間総和クエリ(RSQ)や区間最大値クエリ(RMQ)等の従来の出力クエリ
- 区間を覆う各ノードの最大値に関する情報と非最大値に関する情報を合算した上で解を出力
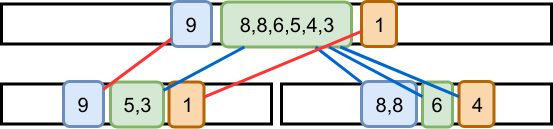
この分割における区間chminクエリの処理イメージは以下の図のようになる。
((厳密な)二番目の最大値) < < (最大値) を満たすノードに対し、青枠(最大値)の要素に差分の加算処理を行った上で最大値に関する情報のみを(区間加算操作として)更新する。

で更新した例 (赤色が即更新、黄色が遅延させて更新)
具体的な例として、上の例題では以下の処理を行うことになる。
pushdownとupdateについて
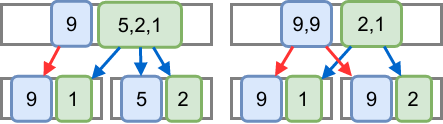
情報を最大値・非最大値に分けて管理する場合、pushdownやupdateの時に区間の最大値・非最大値の関係を考慮しながら伝搬する必要があり、この伝搬関係は左右の子ノードの最大値の値によって決まる。
updateでは、親ノードの情報は左右の子ノードの最大値・非最大値の情報(合わせて4種類の情報)を元に更新する。
具体的に、最大値に関する情報は 左右の子ノードのうち、より大きい最大値を持つ子ノードの最大値の情報から更新する。この時、両方同じ最大値を持つ場合は両方の最大値の情報をマージして更新する。非最大値に関する情報は、それ以外の情報をマージして更新する。

(左図は "左子ノードの最大値 > 右子ノードの最大値"、右図は "左子ノードの最大値 = 右子ノードの最大値")
例えば、上の例題のように最大値の総和と非最大値の総和
を管理している時に、子ノードの各総和から親ノードの各総和をupdateする場合を考える。
この時、左右の子ノードの最大値によって以下のように場合分けしてupdateする。
- 左子ノードの最大値 > 右子ノードの最大値
- 親ノードの
= 左子ノードの
- 親ノードの
= 左子ノードの
+ 右子ノードの
- 親ノードの
- 左子ノードの最大値 < 右子ノードの最大値
- 親ノードの
= 右子ノードの
- 親ノードの
= 左子ノードの
+ 右子ノードの
- 親ノードの
- 左子ノードの最大値 = 右子ノードの最大値
- 親ノードの
= 左子ノードの
+ 右子ノードの
- 親ノードの
= 左子ノードの
+ 右子ノードの
- 親ノードの
pushdownにおける遅延値(lazy tag)の伝搬はupdateの逆方向に行う。
最大値に関する遅延値は、左右の子ノードのうち親ノードと等しい最大値を持つ子ノードへ(最大値が等しい場合は両方へ)伝搬させる。それ以外には、非最大値に関する遅延値を伝搬させる。
(左図は "左子ノードの最大値 > 右子ノードの最大値"、右図は "左子ノードの最大値 = 右子ノードの最大値")
最大値に関する遅延値として の最大値の差分のみを子ノードに伝搬すればよい場合は、pushdownで
の最大値を更新する際の差分の値で伝搬できるため、最大値の差分加算を遅延させるための別のlazy tagを持って処理する必要はない。
例題の実装
上の例題の実装を一応載せておく。
基本的に区間の情報を分割する前に比べて、総和を分割しただけの実装になる。
計算量は
実装コード(Gist): Segment Tree Beatsの例題実装 (Task 3, Task 4まわり) · GitHub
区間chmin/chmaxクエリを扱う問題
区間chmin/chmaxクエリ両方を扱う問題でも同様に区間の情報を分けて解くことができ、最大値・最小値・それ以外の3種類に分けることができる。
この時注意すべきなのは区間の要素が (最大値) = (最小値) のケースで、特別に最大値と最小値に同じ要素が含まれると考える。このケースの実装では、要素を重複して解に含めないように注意する。(総和で要素を2回足す、など)
updateやpushdownも区間chminクエリのみの場合と同じ考え方で処理する
- update:
- 親ノードの最大値(最小値)の情報は、左右の子ノードの中での最大値(最小値)の情報から更新する
- それ以外の要素の情報は、左右の子ノードの中での最大値・最小値以外の情報をマージして更新する
- pushdown:
- 親ノードの最大値(最小値)に関する遅延値は、左右の子ノードで等しい最大値(最小値)を持つ子ノードへ伝搬する
- それ以外には、非最大値かつ非最小値の要素に関する遅延値を伝搬する
値が変更されるたびに1加算する (Task 3)
長さ
の数列
が与えられる。また、最初全て0の長さ
の数列
が与えられる。
以下のクエリを合計回処理せよ。
について
の値を
に更新
について
の値を
に更新
について
の値を
に更新
の値を出力
- (各クエリ後、そのクエリで
の値が変わった全ての
について、
に1を加算)
制約:
数列をクエリで処理するたびに数列
の値が増加する問題。
この問題ではの区間総和に答えるために、各ノードでは
の区間総和を管理する。
区間加算クエリ(RAQ)のみであれば、の場合に区間内の
に1を一様に加算すればよい。しかし区間chminクエリは
を満たす全ての
について
に1を加算する必要がある。
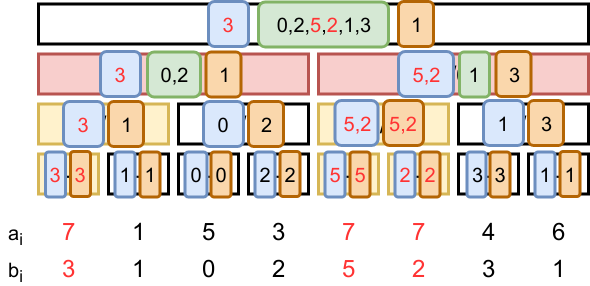
ここで各ノードにおいて以下のように を3種類に分け、それぞれの総和を管理することを考える。
すると区間chmin(chmax)クエリにおける の更新処理は、各ノードの
の最大値(最小値)が変化した時に、最大値(最小値)に関する全ての
に(遅延させながら)1を一様加算する処理になり、その分を総和
(
)に加算すればよくなる。

(枠内はの値を示し、この枠単位の総和
を管理する)
この更新に合わせても更新する
実装的には、この問題では総和を分けて管理する必要性はないため、各ノードでは全ての総和の和 の値を管理すればよい。
また、区間加算クエリは区間に含まれる全てのに1を一様加算するだけになる。
そのため、遅延させながら一様加算するための遅延値として
の3種類を管理すればよい。
計算量は
実装コード
全体の実装(Gist): Segment Tree Beatsの例題実装 (Task 3, Task 4まわり) · GitHub
区間chminクエリを含む、2つの値の和の最大値を扱う (Task 4)
2つの数列と
の各
における和
の区間最大値を扱う問題。
Task 4では両方の数列で区間chminクエリを扱うが、まずは簡単な例として片方のみが区間chminクエリを扱う例を考えてみる。
1つの数列のみで区間chminクエリを処理する問題
長さ
の数列
と数列
が与えられる。以下のクエリを合計
回処理せよ。
について
の値を
に更新
について
の値を
に更新
を出力
制約:
この問題では の最大値が必要となるため、この情報を各ノードで維持する必要がある。
もし数列が従来の区間操作(RAQ, RUQ)のみであれば、
に関して区間最大値のみを持つことで処理できる。
しかし区間chminクエリでは となる
だけ
の値を更新するため、(遅延させて更新する関係上)
に関して区間最大値のみ持つだけでは処理できない。例えば、
が小さくなることで
が更新されなかった
が新たな最大値になる場合があり、これを考慮するのは難しい。
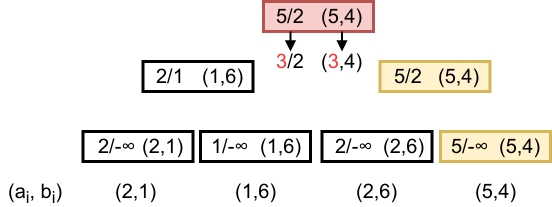
の最大値のみを管理した時に更新に失敗するケース
(区間のを
で更新した際、
の区間最大値を8 (=2+6)に更新できない)
そこでが非最大値の時の
の区間最大値も考慮できるように、
が最大値の時と非最大値の時で区間情報を分けて管理することを考える。
具体的に、各ノードで以下のペア情報を管理する。(ペアではなく の値をそのまま持っても処理できるが、今回はペアで持って処理する)
以下の図は数列、数列
における各ノードの管理イメージである。"×"の箇所は該当するペアが存在しないことを意味しており、実装では
を保持させる。
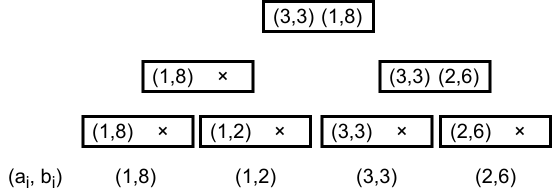
(各ノードの左が、右が
)
そして以下のように処理する。
の区間chminクエリ:
- 更新対象となるノードにおける、
に含まれる
を
に更新
- 更新対象となるノードにおける、
の区間更新クエリ(RUQ):
- 更新区間に含まれる全てのノードについて
に含まれる
を
に更新
の
を二番目の最大値、
を
に更新
- 更新区間に含まれる全てのノードについて
の区間最大値クエリ:
- 区間を覆う各ノードについて
と
から
の最大値を求め、全てのノードにおける最大値を出力
- 区間を覆う各ノードについて
計算量は
実装コード
全体の実装(Gist): Segment Tree Beatsの例題実装 (Task 3, Task 4まわり) · GitHub
区間chminクエリが処理される2つの列を処理する問題
次に本題であるTask4を考えてみる。
長さ
の数列
と数列
が与えられる。以下のクエリを合計
回処理せよ。
について
の値を
に更新
について
の値を
に更新
について
の値を
に更新
について
の値を
に更新
を出力
制約:
一つ前の例のように の区間最大値を扱えるようにするために、各数列
、
がそれぞれ最大値・非最大値の場合に分けて管理することで解くことができる。
具体的に と
の最大値・二番目の最大値に加えて、各ノードでは以下の4種類のペア
の情報を管理する。(これも同様に
の値をそのまま持っても処理できる)
と
が最大値となる
の中で
が最大値となるペア
が最大値、
が非最大値となる
の中で
が最大値となるペア
が非最大値、
が最大値となる
の中で
が最大値となるペア
と
が非最大値となる
の中で
が最大値となるペア
以下の図は数列、数列
を
が最大となる4種類のペアを管理するイメージである。
("×"の箇所は該当するペアが存在しないことを示し、値としてはを保持させる)
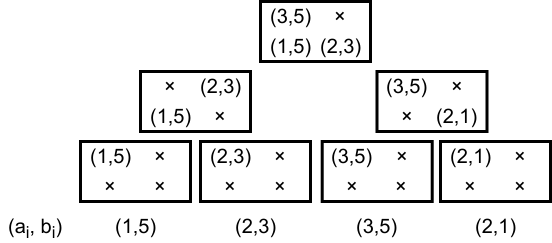
(各ノードの左上が、右上が
、左下が
、右下が
)

(赤枠: に対する区間chminクエリで更新するペア, 青枠:
に対する区間chminクエリで更新するペア)
数列に対する区間chminクエリでは
が最大値となる
と
の
の値を更新し(上図の赤枠)、数列
に対する区間chminクエリでは
が最大値となる
と
の
を更新する(上図の青枠)。
数列と数列
に対する区間加算クエリでは、全てのペアの
、
の値を更新すればよい。
そして、の最大値を出力する際は、区間内の4種類のペアの中の
の最大値を出力すればよい。
計算量は