Segment Tree Beatsの実装メモ (Historic Informationまわり)

Segment Tree Beats(SGT Beats)のHistoric Informationまわりについて自分が理解した範囲のメモ

この記事は以下の続き。これらの説明を前提に書いてある。

また、以下を参考にしてこの記事を書いている。

A simple introduction to "Segment tree beats" - Codeforces (Task 5, Task 6あたり)
区间最值操作与历史最值问题 - 道客巴巴 (主に4.4, 4.5あたり)

Historic Information
historic maximal/minimal valueを管理する考え方
historic sumを管理する考え方
- 実装
- 区間chmin/chmaxクエリを含む場合
区間chmax(chmin)クエリを含むhistoric maximal valueを扱う
区間chmin/chmaxクエリを同時に処理するhistoric maximal valueを扱う
- 実装
RUQを含むhistoric informationを処理する
関連問題

Historic Information

Segment Tree Beatsで処理できるものにHistoric Informationがある。

$a_i$ に対する区間加算クエリや区間chmin/chmaxクエリを処理しながら以下を処理できる。

historic maximal value:
- 各 ${a_i}$ における、現在までの最大の ${a_i}$ の値 ${b_i}$ を管理
- $b_i$ の区間最大値・最小値、区間総和を求める
historic minimal value:
- 各 ${a_i}$ における、現在までの最小の ${a_i}$ の値 ${c_i}$ を管理
- $c_i$ の区間最大値・最小値、区間総和を求める
historic sum:
- 各 ${a_i}$ に対し ${s_i}$ を管理し、各クエリごとに全ての $i$ について ${s_i \leftarrow s_i + a_i}$ で更新
- $s_i$ の区間総和を求める

従来の遅延セグ木でもある程度であれば実現できる。例えば、以下のようにhistoric maximal valueの区間最大値を管理することができる(区間chmaxクエリも処理できる)。

historic maximal/minimal valueを管理する考え方

historic maximal valueについて扱う。historic minimal valueも同様の考え方で解くことができる。

以下の問題を考える。

長さ ${N}$ の数列 ${A}$ が与えられる。また、最初は数列 $A$ と等しい数列 $B$ がある。
以下のクエリを合計 ${M}$ 回処理せよ。

${l \le i < r}$ について ${a_i}$ を ${a_i + x}$ に更新

$\sum_{l \le i < r} b_i$ を出力

$\max_{l \le i < r} b_i$ を出力

各クエリ後、各 ${b_i}$ は ${\max(b_i, a_i)}$ に更新される。
制約: ${N, M \le 10^5}$

この問題では各 $a_i$ のhistoric maximal valueである $b_i$ を管理する必要がある。
この $b_i$ の代わりに、過去最大値と現在値の差分( ${d_i = b_i - a_i}$ )の列 ${D = d_1, d_2, ..., d_N}$ を管理することを考える。
(下の図の白い部分が ${a_i}$ 、橙色の部分が ${d_i}$ に該当する)

f:id:smijake3:20190421040714p:plain — historic maximal valueのイメージ
黒数字が現在の $a_i$ の値、その下の茶色数字が最大値と現在地の差 ${d_i}$ の値

historic maximal valueのイメージ
黒数字が現在の $a_i$ の値、その下の茶色数字が最大値と現在地の差 ${d_i}$ の値

すると、 ${a_i}$ に ${x}$ を加算する際に ${d_i}$ を ${\max(d_i - x, 0)}$ に更新するのみになる。
(Segment Tree Beats上では区間加算クエリ → 区間chmaxクエリで処理すればよいため簡単に処理できる)

全体の計算量は $O(N \log N + M \log^2 N)$

区間総和クエリ(RSQ)の処理

各要素のhistoric maximal valueは $b_i = a_i + d_i$ と表されるので、区間総和は
$\displaystyle \sum_{l \le i < r} b_i = \sum_{l \le i < r} a_i + \sum_{l \le i < r} d_i$
を求めればよいことになる。

そのため、数列 $A$ の区間総和と数列 $D$ の区間総和を別々に求め、その和を解とすればよい。

区間最大値クエリ(RMQ)の処理

この問題ではhistoric maximal valueの区間最大値を直接管理しても解ける。(区間総和がなければ $O(M \log N)$ )
ここでは、 $a_i, d_i$ をベースに管理することを考えてみる。

historic maximal valueの区間最大値は
$\displaystyle \max_{l \le i < r} b_i = \max_{l \le i < r} (a_i + d_i)$
を求めることになる。

この区間最大値は前回の例題のTask4と同じ感じで処理することができ、各ノードで以下の区間情報を持たせることで解くことができる。

が最小値となるの中のの最大値
- 最小値の $d_i$ をchmaxで更新する際に加算処理が行われる
$d_i$ が非最小値となる $i$ の中の $a_i + d_i$ の最大値

同様の考え方で $b_i$ の区間最小値クエリも処理できる。

実装

実装コード(Gist): Segment Tree Beats (Historic Informationまわり) の実装 · GitHub

historic sumを管理する考え方

以下のような問題を考える。

長さ ${N}$ の数列 ${A}$ が与えられる。また、最初は数列 ${A}$ と等しい数列 ${S}$ がある。
以下のクエリを合計 ${M}$ 回処理せよ。

${l \le i < r}$ について ${a_i}$ を ${a_i + x}$ に更新

$\sum_{l \le i < r} s_i$ を出力

各クエリ後、各 ${s_i}$ は ${s_i + a_i}$ に更新される。
制約: ${N, M \le 10^5}$

現在処理しているクエリ番号を ${t}$ ( $t = 0, 1, ..., M-1$ )とする。
historic sumを管理するために、数列 ${A}$ とは別に、各 $i$ について ${s_i = a_i \times t + b_i}$ を満たす数列 ${B = b_1, ..., b_N}$ を管理することを考える。

$t$ 番目が区間加算クエリで ${a_i}$ を ${a_i + x}$ に更新した場合、 ${s_i}$ が ${s_i + (a_i + x)}$ に更新されるため、これに合うように ${b_i}$ を ${b_i - x \times t}$ に更新すればよい。
この $b_i$ の更新は区間加算操作によって実現できる。

また、 $t$ 番目で区間総和クエリ(RSQ)を処理する場合、
$\displaystyle \sum_{l \le i < r} s_i = t \times \sum_{l \le i < r} a_i + \sum_{l \le i < r} b_i$
で求められるため、( $A$ 上のRSQ) × $t$ + ( $B$ 上のRSQ)で求めることができる。

この問題では、数列 $A$ と数列 $B$ に対してRAQとRSQができれば十分である。そのため、2つの数列に対してRAQとRSQを処理できる従来の遅延セグ木もしくは BIT で解くことができる。

計算量は $O(M \log N)$

実装

実装コード(Gist): Segment Tree Beats (Historic Informationまわり) の実装 · GitHub

区間chmin/chmaxクエリを含む場合

この場合のhistoric sumも簡単に処理できる。
例えば区間chminクエリを処理する際、(二番目の最大値) < x < (最大値)を満たすノードで最大値となる $a_i$ に加算されたら、それに合わせて $b_i$ にも加算するだけでよい。

区間chmax(chmin)クエリを含むhistoric maximal valueを扱う

以下のような問題を考える。

長さ ${N}$ の数列 ${A}$ が与えられる。以下のクエリを合計 ${M}$ 回処理せよ。

$l \le i < r$ について ${a_i}$ を $\max(a_i, x)$ に更新

${l \le i < r}$ について ${a_i}$ を ${a_i + x}$ に更新

$\displaystyle \max_{l \le i < r} b_i$ を出力

$\displaystyle \sum_{l \le i < r} b_i$ を出力

各クエリ後、各 ${b_i}$ は ${\max(b_i, a_i)}$ に更新される。
制約: ${N, M \le 10^5}$

今回も前の例のように数列 $A$ の値に加え、 (過去最大値) - (現在値)を示す数列 $D$ の値を管理する。

この問題では、数列 $D$ に対して以下の処理を実現する必要がある

区間加算クエリ:
- 更新区間内の全ての $d_i$ について ${\max(d_i - x, 0)}$ に更新
区間chmaxクエリ:
- 更新区間内で $a_i (< x)$ が更新される $i$ のみについて $a_i$ の最小値の更新前後の差分 $c = x - a_i$ を用いて $d_i$ を ${\max(d_i - c, 0)}$ に更新

問題は(2)の処理であり、 $a_i$ に対し区間chmaxクエリを処理する際に (最小値) < x < (二番目の最小値) を満たす各ノードにおいて $a_i$ が最小となる全ての $d_i$ のみに加算とchmax を行う必要がある。
そのため、前の例のように各ノードで単に $d_i$ の最小値・二番目の最小値を管理するだけではうまく更新できない。

そこで、 $a_i$ が最小値となる $d_i$ のみを更新できるように、各ノードにおいて $a_i$ が最小値となる場合と $a_i$ が非最小値となる場合とで $d_i$ の区間情報を分けて管理することを考える。
具体的に、各ノードに以下の区間情報をもたせる。

$a_i$ が最小値となる $i$ の中での、 ${d_i}$ の最小値、二番目の $d_i$ の最小値、最小値の個数
$a_i$ が非最小値となる $i$ の中での、 ${d_i}$ の最小値、二番目の $d_i$ の最小値、最小値の個数

ここで具体的な例で考えてみる。以下の図は今回の例とするセグ木である。
各ノードには $a_i$ の最小値・二番目の最小値が書かれてある。(この後の図では $a_i$ の最小値を省略するので、分かりやすさのために $a_i$ が最小値が同じ箇所を同じ色で塗り分けてある)

f:id:smijake3:20190601141801p:plain — セグ木で管理する例

そして、以下の図は $d_i$ の要素を $a_i$ の最小値・非最小値で分けて管理する例である。 $a_i$ が最小値の場合(青枠)と非最小値の場合(緑枠)で分けて $d_i$ の最小値・二番目の最小値を管理するイメージである。
各枠の"x/y"はxが最大値、yが二番目の最大値(yが書かれてない場合は $+\infty$ )を示す。枠が存在しない場合はx,yそれぞれ $+\infty$ を示す。

f:id:smijake3:20190601141848p:plain — セグ木上で $a_i$ の最小値・非最小値で $d_i$ の最小値・非最小値を分離して管理するイメージ

セグ木上で $a_i$ の最小値・非最小値で $d_i$ の最小値・非最小値を分離して管理するイメージ

このように管理することで、区間chmaxクエリも処理できるようになる。

実際に各操作クエリでは以下の処理を行えばよい

区間加算操作(, )を行う
- 区間chmaxクエリ: $a_i$ の最小値を更新するノードにおいて、 $a_i$ が最小値となる全ての $i$ に加算操作
- 区間加算クエリ: 区間内の全ての $i$ に加算操作
をで更新する
- $a_i$ が最小値となる $d_i$ 、 $a_i$ が非最小値となる $d_i$ それぞれについて ( $d_i$ の最小値) < 0 < ( $d_i$ の二番目の最小値) を満たすノードまで探索して $d_i$ の最小値を 0 で更新する

ここで、例のセグ木を $a_i \leftarrow \max(a_i, 5)$ で更新する例を考える。
初めに ( $a_i$ の最小値) < 5 < ( $a_i$ の二番目の最小値) となるノードの $a_i$ 最小値とその $d_i$ を加算操作で更新する。(赤丸の"+x"は $a_i$ が最小値となる $d_i$ への一様加算を示す)

f:id:smijake3:20190601142005p:plain — a_i を max(a_i, 5) で更新する例 (a_i と d_i に対する加算操作)

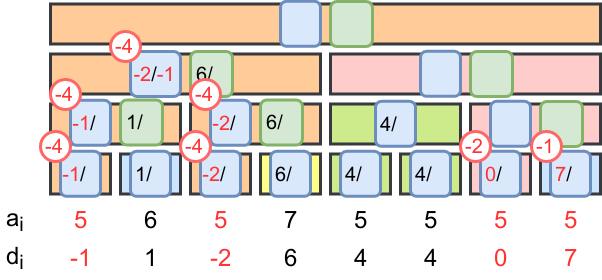
この加算操作の後、更に( $a_i$ が最小値・非最小値の場合それぞれで) ( $d_i$ の最小値) < 0 < ( $d_i$ の二番目の最小値) となるノードの $d_i$ の最小値を0に更新する。(青丸の"+x"は $a_i$ が最小値の中で $d_i$ の最小値のみへの加算を示す)

f:id:smijake3:20190601142032p:plain — a_i を max(a_i, 5) で更新する例 (d_i の更新操作)

全体の計算量は $O(N \log^2 N +M \log^3 N)$ になることが示せる。

区間総和クエリ(RSQ)の処理

区間総和の管理は前の例とほぼ同じで、各ノードで数列 $A$ と数列 $D$ の区間総和を管理し、 $a_i$ と $d_i$ の一様加算の処理に応じて区間総和を変化させればよい。

区間最大値クエリ(RMQ)の処理

区間chmaxクエリを含まない例題と同じように各ノードで $a_i + d_i$ の値を( $d_i$ が最小値・非最小値で分けて)管理する。

今回は区間chmaxクエリで処理できるように、 $a_i$ が最小値・非最小値の場合に分けた上で $d_i$ が最小値・非最小値の場合で分けて管理する。

以下の図は $a_i + d_i$ の最大値を管理するイメージを示したもの。 $a_i$ が最小値(青枠)と非最小値(緑枠)の中それぞれで、 $d_i$ が最小値/非最小値の時の $a_i + d_i$ の最大値を保持する。
各枠の"x/y"は x が $d_i$ が最小値の時、yが $d_i$ が非最小値の時の $a_i + d_i$ の最大値を示す。(書かれてない場合は $-\infty$ を表す)

f:id:smijake3:20190522090644p:plain — $a_i + d_i$ の最大値を管理するイメージ
(省略されている箇所は $-\infty$ を保持する)

この問題の区間総和がなければ、従来の遅延セグ木でうまくマージできるlazy tagを定義できるため $O(M \log N)$ で解くことができる。もしlazy tagがうまくマージできない場合(今回の問題が区間chminクエリだった場合等)でも、現在の最大値とhistoric maximal valueを $a_i$ が最大値の場合・ $a_i$ が非最大値の場合、等で分けて管理することで $O(N \log N + M \log^2 N)$ で解くことができる。

実装

各ノードが持つ区間情報

// d_i まわりの情報を管理する構造体
// 各ノードごとに、この構造体を a_i が最小値の場合・a_i が非最小値の場合 で2つ持つ
struct HistVal {
  //  min_v: d_i の最小値
  // smin_v: 二番目の最小値
  //  min_c: 最小値の個数
  //    sum: d_iの総和
  ll min_v, smin_v, min_c, sum;

  //  m_hmax: d_i が最小値の a_i + d_i の最大値
  // nm_hmax: d_i が非最小値の a_i + d_i の最大値
  ll m_hmax, nm_hmax;

  // ...

  // d_i の最小値を x に更新
  // pushdown, chmaxの際に使う
  void update_min(ll x) {
    if(min_v < x) {
      sum += (x - min_v) * min_c;
      // a_i + d_i の最大値はここのみで変化する
      m_hmax += (x - min_v);

      min_v = x;
    }
  }

  // l と r の2つの d_i の情報をマージして更新
  // updateの際に使う
  // (l もしくは r に自身を指定しても問題ないように実装してある)
  void merge(HistVal &l, HistVal &r) {
    sum = l.sum + r.sum;
    nm_hmax = max(l.nm_hmax, r.nm_hmax);

    if(l.min_v < r.min_v) {
      smin_v = min(l.smin_v, r.min_v);
      min_v = l.min_v;
      min_c = l.min_c;

      nm_hmax = max(nm_hmax, r.m_hmax);
      m_hmax = l.m_hmax;
    } else if(l.min_v > r.min_v) {
      smin_v = min(l.min_v, r.smin_v);
      min_v = r.min_v;
      min_c = r.min_c;

      nm_hmax = max(nm_hmax, l.m_hmax);
      m_hmax = r.m_hmax;
    } else {
      min_v = l.min_v;
      smin_v = min(l.smin_v, r.smin_v);
      min_c = l.min_c + r.min_c;

      m_hmax = max(l.m_hmax, r.m_hmax);
    }
  }

  // 要素にxを加算
  void add(ll x) {
    if(min_v != inf) min_v += x;
    if(smin_v != inf) smin_v += x;
  }

  // a_i + d_i の区間最大値を返す
  ll hmax() {
    return max(m_hmax, nm_hmax);
  }
};

//  min_d: a_i が最小値の i における d_i まわりの情報
// nmin_d: a_i が非最小値の i における d_i まわりの情報
HistVal min_d[4*N], nmin_d[4*N];

// 区間加算クエリ用 (ladd: lazy tag, len: 区間要素数)
ll len[4*N], ladd[4*N];

// a_i の最小値・二番目の最小値・最小値の個数
ll min_v[4*N], smin_v[4*N], min_c[4*N];
// a_i の区間総和
ll sum[4*N];

// ノードk の
// - b_i の区間総和: sum[k] + min_d[k].sum + nmin_d[k].sum
// - b_i の区間最大値: max(min_d[k].hmax(), nmin_d[k].hmax())

区間chmaxクエリを処理するための実装

// a_i の最小値を x に更新する
void update_node_min(int k, ll x) {
  // a_i の区間総和の更新
  sum[k] += (x - min_v[k]) * min_c[k];

  // d_i に関する情報の更新
  // a_i が最小値となる場合の d_i を更新
  min_d[k].add(min_v[k] - x);
  min_d[k].sum += (min_v[k] - x) * min_c[k];

  min_v[k] = x;
}

// 区間[a, b) の a_i を max(a_i, x) に更新
void _update_max(ll x, int a, int b, int k, int l, int r) {
  if(b <= l || r <= a || x <= min_v[k]) {
    return;
  }
  if(a <= l && r <= b && x < smin_v[k]) {
    update_node_min(k, x);
    // d_i の値を max(d_i, 0) で更新
    _update_dmax(k, l, r);
    return;
  }

  push(k);
  _update_max(x, a, b, 2*k+1, l, (l+r)/2);
  _update_max(x, a, b, 2*k+2, (l+r)/2, r);
  update(k);
}

区間加算クエリを処理するための実装

void addall(int k, ll a) {
  // a_i に関する情報を更新
  min_v[k] += a;
  if(smin_v[k] != inf) smin_v[k] += a;
  sum[k] += a * len[k];

  // d_i に関する情報を更新
  // a_i が最小値の場合・非最小値の場合、両方の d_i を更新
  min_d[k].add(-a); nmin_d[k].add(-a);
  min_d[k].sum -= a * min_c[k];
  nmin_d[k].sum -= a * (len[k] - min_c[k]);

  // 遅延させている値の更新
  ladd[k] += a;
}

// 区間[a, b) の a_i を a_i + x に更新
void _add_val(ll x, int a, int b, int k, int l, int r) {
  if(b <= l || r <= a) {
    return;
  }
  if(a <= l && r <= b) {
    addall(k, x);
    // d_i の値を max(d_i, 0) で更新
    _update_dmax(k, l, r);
    return;
  }
  push(k);
  _add_val(x, a, b, 2*k+1, l, (l+r)/2);
  _add_val(x, a, b, 2*k+2, (l+r)/2, r);
  update(k);
}

d_i に対する区間chmax更新処理

DFS中の条件は以下のように設定すればよい

break condition: $a_i$ が最大値・非最大値の場合両方で 0 ≤ ( $d_i$ の最小値) を満たす
tag condition: $a_i$ が最大値・非最大値の場合両方で0 < ( $d_i$ の二番目の最小値) を満たす

// (内部用) d_i <- max(d_i, 0) で更新
void _update_dmax(int k, int l, int r) {
  // break condition: 以下の条件を満たすこと
  // - a_i が最小値である d_i の最小値(min_d[k].min_v)が0以上
  // - a_i が非最小値である d_i の最小値(nmin_d[k].min_v)が0以上
  if(l == r || (0 <= min_d[k].min_v && 0 <= nmin_d[k].min_v)) {
    return;
  }
  // tag condition: 以下の条件を満たすこと
  // - a_i が最小値である d_i の二番目の最小値(min_d[k].smin_v)が0より大きい
  // - a_i が非最小値である d_i の二番目の最小値(nmin_d[k].smin_v)が0より大きい
  if(0 < min_d[k].smin_v && 0 < nmin_d[k].smin_v) {
    // d_i の最小値を 0 に更新する
    min_d[k].update_min(0);
    nmin_d[k].update_min(0);
    return;
  }

  push(k);
  _update_dmax(2*k+1, l, (l+r)/2);
  _update_dmax(2*k+2, (l+r)/2, r);
  update(k);
}

pushdown処理

$a_i$ が最小値の場合・非最小値の場合で情報を分けて管理しているため、正しく伝搬を行う。

$a_i$ が最小値の場合の $d_i$ の最小値は、左右の子ノードで $a_i$ が最小値となる方に伝搬する。
それ以外は $a_i$ が非最小値の場合の $d_i$ の最小値を伝搬する。

void push(int k) {
  if(ladd[k] != 0) {
    addall(2*k+1, ladd[k]);
    addall(2*k+2, ladd[k]);
    ladd[k] = 0;
  }
  if(min_v[2*k+1] < min_v[k]) {
    update_node_min(2*k+1, min_v[k]);
  }
  if(min_v[2*k+2] < min_v[k]) {
    update_node_min(2*k+2, min_v[k]);
  }

  // 子ノードにおける a_i が最小値の場合の d_i の最小値に、ノードkの d_i の最小値情報を伝搬
  // - 子ノードにおける a_i の最小値の大小関係によって、
  //   どちらの d_i の最小値(min_d[k].min_v, nmin_d[k].min_v)を伝搬するか決める
  if(min_v[2*k+1] < min_v[2*k+2]) {
    min_d[2*k+1].update_min(min_d[k].min_v);
    min_d[2*k+2].update_min(nmin_d[k].min_v);
  } else if(min_v[2*k+1] > min_v[2*k+2]) {
    min_d[2*k+1].update_min(nmin_d[k].min_v);
    min_d[2*k+2].update_min(min_d[k].min_v);
  } else { // min_v[2*k+1] == min_v[2*k+2]
    min_d[2*k+1].update_min(min_d[k].min_v);
    min_d[2*k+2].update_min(min_d[k].min_v);
  }

  // a_i の非最小値の場合の d_i の最小値に情報を伝搬
  nmin_d[2*k+1].update_min(nmin_d[k].min_v);
  nmin_d[2*k+2].update_min(nmin_d[k].min_v);
}

update処理

$a_i$ が最小値の場合の $d_i$ の情報は、左右の子ノードの内 $a_i$ の最小値を持つ方のノードから持ってくる。
それ以外の情報は $a_i$ が非最小値となる場合の $d_i$ の情報としてマージする。

void update(int k) {
  sum[k] = sum[2*k+1] + sum[2*k+2];

  nmin_d[k].merge(nmin_d[2*k+1], nmin_d[2*k+2]);

  if(min_v[2*k+1] < min_v[2*k+2]) {
    min_v[k] = min_v[2*k+1];
    min_c[k] = min_c[2*k+1];
    smin_v[k] = min(smin_v[2*k+1], min_v[2*k+2]);

    min_d[k] = min_d[2*k+1];
    nmin_d[k].merge(nmin_d[k], min_d[2*k+2]);
  } else if(min_v[2*k+1] > min_v[2*k+2]) {
    min_v[k] = min_v[2*k+2];
    min_c[k] = min_c[2*k+2];
    smin_v[k] = min(min_v[2*k+1], smin_v[2*k+2]);

    min_d[k] = min_d[2*k+2];
    nmin_d[k].merge(nmin_d[k], min_d[2*k+1]);
  } else { // min_v[2*k+1] == min_v[2*k+2]
    min_v[k] = min_v[2*k+1];
    min_c[k] = min_c[2*k+1] + min_c[2*k+2];
    smin_v[k] = min(smin_v[2*k+1], smin_v[2*k+2]);

    min_d[k].merge(min_d[2*k+1], min_d[2*k+2]);
  }
}

実装全体

実装コード(Gist): Segment Tree Beats (Historic Informationまわり) の実装 · GitHub

区間chmin/chmaxクエリを同時に処理するhistoric maximal valueを扱う

長さ ${N}$ の数列 ${A}$ が与えられる。以下のクエリを合計 ${M}$ 回処理せよ。

$l \le i < r$ について ${a_i}$ を $\max(a_i, x)$ に更新

$l \le i < r$ について ${a_i}$ を $\min(a_i, x)$ に更新

${l \le i < r}$ について ${a_i}$ を ${a_i + x}$ に更新

$\displaystyle \max_{l \le i < r} b_i$ を出力

$\displaystyle \sum_{l \le i < r} b_i$ を出力

各クエリ後、各 ${b_i}$ は ${\max(b_i, a_i)}$ に更新される。
制約: ${N, M \le 10^5}$