Li Chao Treeのメモ

Li Chao (Segment) Treeについて理解をまとめた

以下の問題で使ったので、関連してきちんとまとめようと思った
smijake3.hatenablog.com

参考ページは以下
Convex hull trick and Li Chao tree - Competitive Programming Algorithms

目次

Li Chao Treeとは

Convex Hull Trickとして解くアルゴリズムの1つで、直線をセグメント木で管理しながら、ある点における最小値(最大値)を計算する。
セグメント木のうちの区間では、の区間で最小(最大)の値をとり得る直線が保持される。

そして、計算する座標xが個あるとき、直線追加と最小値(最大値)計算が1回で行える。

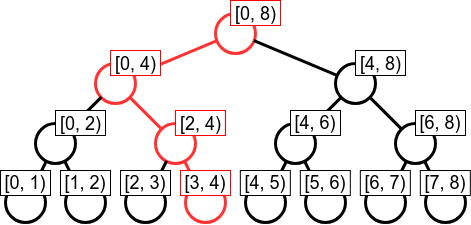
Li Chao Treeにおける最小値の計算

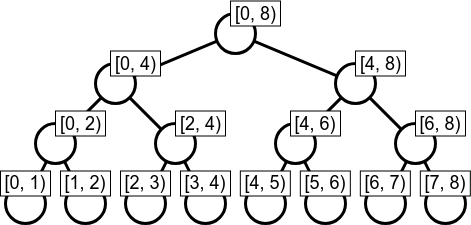
ここでは、２つのクエリ処理、直線追加とある点xにおける最小値を計算する例について説明する。セグメント木はの要素に対しての方が計算しやすいため、とする。

今回、の個の座標xにおける最小値を計算するとする。(任意の区間に対しても動的セグメント木で計算できるが、今回は省略)
各区間では、の範囲で最小値をとり得る直線の式(つまり、)を保持する。保持する情報はのである。全ての区間において、始めはを持つとする。

直線追加

例えば、新たに直線を追加するとする。
区間からトップダウンに探索を行い、その探索で訪れる各区間に既に存在する直線と、現在持っている直線とを比較し、交わる関係によってはとを交換しながら更新を行う。

具体的に、区間に存在する関数と現在持っている関数について、とし、のそれぞれで2つの関数がとる値を比較し、各ケースに対応する。

値を比較した結果、以下のパターンが考えられる(赤線が、青線がとする)

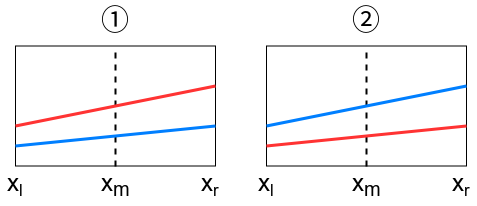
(1)のように、となる場合、は最小値を取れないため、ここでを捨てて更新を終了する。
逆に(2)のように、となる場合、が最小値を取れないため、を区間の関数とし、を捨てて更新を終了する。

(3)もしくは(4)のように、半分の区間もしくは区間でとなる場合、が最小値を取れる区間((3)であれば、(4)であれば)を更に探索する。最小値が取れない方の半分の区間は探索しない。

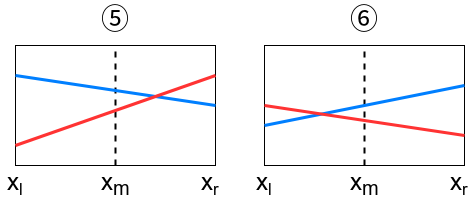
(5)もしくは(6)のように、半分の区間以上でとなる場合、とを交換する。こうすることで、とが逆の関係になり、(3)もしくは(4)のパターンになる。こうすることで、半分の区間を探索するだけになる。

直線追加の実装

これらを踏まえ、直線を追加する処理をPythonで実装したものが以下である。
実際に計算する座標の個数はの形にする必要はあるが、計算上存在しない座標は計算上取り得ない大きい座標にしておけばよい。

# N: 座標の数
# N0 = 2**(N-1).bit_length()
# X[i]: i番目の座標x_i (|X| = N0にする必要あり)

# None: (a, b) = (0, ∞)を表す
data = [None]*(2*N0+1)

# 座標xにおける直線の値f(x)を計算
def f(line, x):
    p, q = line
    return p*x + q

# 区間B = [l, r)の探索
def _add_line(line, k, l, r):
    m = (l + r) // 2
    # 区間Bの直線が(a, b) = (0, ∞)の場合 -> (2)のパターン
    if data[k] is None:
        data[k] = line
        return

    lx = X[l]; mx = X[m]; rx = X[r-1]
    left = (f(line, lx) < f(data[k], lx))
    mid = (f(line, mx) < f(data[k], mx))
    right = (f(line, rx) < f(data[k], rx))

    # (2)のパターン
    if left and right:
        data[k] = line
        return
    # (1)のパターン
    if not left and not right:
        return
    if mid:
        # (5), (6)のパターン -> 区間Bの直線と交換して(3), (4)のパターンに変更
        data[k], line = line, data[k]
    if left != mid:
        # (3)のパターン: [l, m)の探索
        _add_line(line, 2*k+1, l, m)
    else:
        # (4)のパターン: [m, r)の探索
        _add_line(line, 2*k+2, m, r)

def add_line(line):
    return _add_line(line, 0, 0, N0)

最小値計算

ある座標における最小値を計算する際は、座標を含む区間が持つ各関数についてを計算し、それらの値のうちの最小値を求めればよい。

例えば、の最小値を計算するのであれば、以下のように区間が持つ関数の値を計算して最小値を求める。

最小値計算の実装

Pythonにおける最小値計算の実装は以下になる。

def query(k):
    k += N0-1
    x = X[k]
    s = 1e30
    while k >= 0:
        if data[k]:
            s = min(s, f(data[k], x))
        k = (k - 1) // 2
    return s

線分の最小値計算

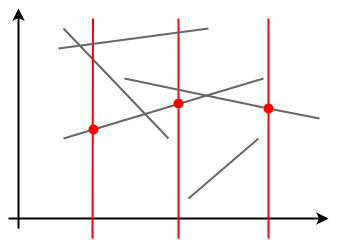
Li Chao Treeにおける直線追加処理を変更することで、線分の最小値(最大値)計算もできるようになる。具体的には、直線追加では全体の区間に対して更新をかけていたが、これを区間に制限し、部分的に更新するようにすればよい。
例えば、下の例のように区間の範囲のみに含まれる(に存在する)線分を更新する場合、区間に直線を追加する処理を行えばよい。

かかる直線追加処理を、高々個の部分区間へ行うため、1回の線分追加処理はになる。

線分追加の実装

従来の直線追加処理を少し変更して線分追加処理に変更したPython実装は以下のようになる。
トップダウンに探索を行い、追加対象の区間が見つかった場合にその区間への直線追加処理を行う。

# N: 座標の数
# N0 = 2**(N-1).bit_length()
# X[i]: i番目の座標x_i (|X| = N0にする必要あり)

data = [None]*(2*N0+1)

def f(line, x):
    p, q = line
    return p*x + q

# 区間B = [l, r)の探索
def _add_line(line, a, b, k, l, r):
    if r <= a or b <= l:
        # 区間[a, b)に到達できない場合は探索を打ち切る
        return
    m = (l + r) // 2
    if not (a <= l and r <= b):
        # 区間[l, r)の部分区間として[a, b)が含まれる
        # => [l, m) と [m, r)に分けてそれぞれ探索を行う
        _add_line(line, a, b, 2*k+1, l, m)
        _add_line(line, a, b, 2*k+2, m, r)
        return
    # ここ以降は、[a, b)の区間に[l, r)が含まれている場合の処理
    # (直線追加処理と同じ)

    if data[k] is None:
        data[k] = line
        return

    lx = X[l]; mx = X[m]; rx = X[r-1]
    left = (f(line, lx) < f(data[k], lx))
    mid = (f(line, mx) < f(data[k], mx))
    right = (f(line, rx) < f(data[k], rx))

    if left and right:
        data[k] = line
        return
    if not left and not right:
        return
    if mid:
        data[k], line = line, data[k]
    if left != mid:
        _add_line(line, a, b, 2*k+1, l, m)
    else:
        _add_line(line, a, b, 2*k+2, m, r)

def add_line(line, a, b):
    return _add_line(line, a, b, 0, 0, N0)

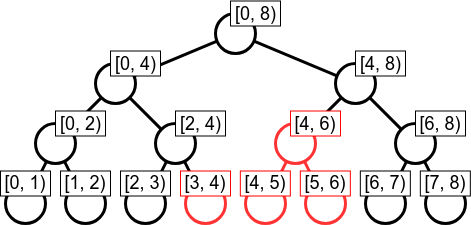
線分追加の実装(高速化)

高速化するのであれば、トップダウン探索で追加対象の区間へ移動するのではなく、区間となる区間を列挙して、直接直線を追加するとよい。(Pythonだとこれが結構効く)

# N: 座標の数
# N0 = 2**(N-1).bit_length()
# X[i]: i番目の座標x_i (|X| = N0にする必要あり)

data = [None]*(2*N0+1)

def f(line, x):
    p, q = line
    return p*x + q

# _add_lineは直線追加処理から変更なし
def _add_line(line, k, l, r):
    m = (l + r) // 2
    if data[k] is None:
        data[k] = line
        return

    lx = X[l]; mx = X[m]; rx = X[r-1]
    left = (f(line, lx) < f(data[k], lx))
    mid = (f(line, mx) < f(data[k], mx))
    right = (f(line, rx) < f(data[k], rx))

    if left and right:
        data[k] = line
        return
    if not left and not right:
        return
    if mid:
        data[k], line = line, data[k]
    if left != mid:
        _add_line(line, 2*k+1, l, m)
    else:
        _add_line(line, 2*k+2, m, r)

def add_line(line, a, b):
    # 追加する区間[l, l+2^k)を列挙して、区間[l, l+2^k)に直線として追加
    L = a + N0; R = b + N0
    a0 = a; b0 = b
    sz = 1
    while L < R:
        if R & 1:
            R -= 1
            b0 -= sz
            _add_line(line, R-1, b0, b0+sz)
        if L & 1:
            _add_line(line, L-1, a0, a0+sz)
            L += 1
            a0 += sz
        L >>= 1; R >>= 1
        sz <<= 1

関連する問題

直線最小値・最大値

CSAcademy - Squared Ends
AtCoder - D問題: 長方形
No.703 ゴミ拾い Easy - yukicoder

線分最小値・最大値

CodeChef - The Street
CodeChef - Archi and Tree
No.704 ゴミ拾い Medium - yukicoder